Favoriser la numératie précoce en prématernelle et en maternelle

Introduction

Au cours des six dernières décennies, il est devenu de plus en plus clair que les connaissances mathématiques de tous les jours (informelles) des enfants constituent un fondement important pour l’apprentissage des mathématiques à l’école (formelles).^1,2,3 Prenons l’exemple d’une question qui a fait l’objet d’un long débat : comment aider au mieux les élèves à maîtriser les additions (de base) à un chiffre, telles que 3 + 4 = 7 et 9 + 5 = 14, et les soustractions associées, telles que 7 - 3 = 4 et 14 - 9 = 5 (voir par ex. Baroody et Dowker,⁴ en particulier les chapitres 2, 3, 6 et 7)? (La maîtrise de ces opérations implique de générer des sommes et des différences rapidement et avec précision et d’appliquer ces connaissances de manière appropriée et flexible⁵). Les recherches indiquent qu’aider les enfants à développer leur sens des nombres au cours des années préscolaires et primaires peut favoriser la maîtrise des opérations.^6,7,8,9 Le but du présent article consiste à résumer comment le développement d’une perception des nombres informelle avant la maternelle et la première année fourni les bases d'une aptitude gagnante pour maîtriser les procédés de l’addition et de la soustraction en deuxième et troisième année.

Questions clés pour la recherche

1. À quel moment les parents et les éducateurs de la petite enfance doivent-ils commencer (a) le processus consistant à encourager la perception des nombres et (b) les efforts visant à favoriser directement la maîtrise des procédés?
2. Quels sont les éléments préalables relatifs au développement que les enfants de prématernelle et de maternelle ont besoin pour maîtriser les additions et les soustractions de base de façon efficace?
3. Quel est le rôle joué par le langage dans le développement de ces connaissances fondamentales?
4. Comment les parents et les éducateurs de la petite enfance peuvent-ils encourager de la façon la plus efficace possible la perception des nombres et la maîtrise des procédés?

Récents résultats de recherche

Question 1. Le processus consistant à aider les enfants à développer leur perception des nombres, qui représente les fondements de la maîtrise des procédés, peut et doit commencer pendant les années préscolaires. Les études récentes indiquent que les enfants commencent à développer très tôt leur perception des nombres. En fait, certains bambins âgés de seulement 18 mois et presque tous les enfants de 2 ans ont commencé à apprendre les éléments sur le plan du développement qui sont préalables à la maîtrise des procédés (p. ex., voir Baroody, Lai, & Mix,¹ pour une analyse).

La réussite des efforts consistant à encourager la maîtrise des procédés dépend du fait que l’on s’assure que l’enfant est prêt sur le plan du développement et qu’il n’est pas bousculé. Les études indiquent que des différences individuelles importantes sur le plan de la perception des nombres apparaissent dès l’âge de deux ou de trois ans et augmentent souvent avec l’âge;^1,10 il n’existe donc aucune règle ferme concernant le moment où devrait commencer une formation officielle relative à la maîtrise des faits. Cependant, pour de nombreux enfants, il est possible que même avec les sommes les plus simples (n+0 et n+1), une telle formation ne soit pas appropriée sur le plan du développement avant la fin de la maternelle ou le début de la première année.¹¹ Pour les enfants à risque d’échec sur le plan scolaire, il arrive souvent que même les sommes les plus simples n’aient aucun sens avant la première ou la deuxième année.¹²

Questions 2 et 3. Certaines études indiquent que le langage, sous la forme du nom des premiers nombres, joue un rôle clé dans le développement de la perception des nombres (pour obtenir une discussion détaillée, voir Baroody;³ Mix, Sandhofer, & Baroody¹³). Plus spécifiquement, il peut fournir une base pour deux fondements de la perception précoce des nombres, c’est-à-dire le concept de nombre cardinal (le nombre total d’objets dans une collection) et l’aptitude de reconnaissance verbale des nombres, généralement appelée « subitisation », illustrés en haut de la figure 1. La reconnaissance verbale des nombres consiste à percevoir de façon fiable et efficace le nombre d’objets dans des collections peu nombreuses et à désigner celui-ci par le bon nom. L’utilisation de « un », « deux », « trois », conjointement avec la visualisation d’exemples et de contre exemples de chacun peut aider les enfants de 2 et 3 ans à développer un concept de plus en plus fiable et exact des « nombres intuitifs » un, deux et trois, c’est-à-dire une compréhension du concept de un, de deux et de trois. Prenons l’exemple du processus de compréhension du chiffre « deux » :

• En voyant divers exemples de paires tels que 👟👟, 🧸🧸, ⚽️⚽️, et 🖍🖍, toutes désignées par « deux », les jeunes enfants peuvent reconnaître que l’apparence des objets faisant partie des collections n’a aucune importance (la forme et la couleur ne sont pas pertinents pour le nombre). Cela peut également leur fournir un identifiant (« deux ») pour leur concept intuitif de pluralité (plus d’un objet).
• Les contre exemples de paires tels que 👟, 🧸🧸🧸, ⚽️, et 🖍🖍🖍 désignés comme n'étant « pas deux » ou avec le nom d’un autre nombre, peut les aider à définir les limites du concept de deux.

Les implications clés pour l’enseignement sont que la compréhension de base des nombres cardinaux n’est pas innée et qu’elle ne se développe pas automatiquement (cf. Dehaene¹⁵).^14,16 Les parents et les éducateurs de prématernelle sont importants pour fournir les expériences et la rétroaction nécessaires pour développer les concepts numériques. Ils devraient tirer parti des situations porteuses de sens qu’ils rencontrent tous les jours afin de nommer (et d’encourager les enfants) à nommer des collections peu nombreuses (p. ex., « Combien de pieds as-tu? » « Tu as donc besoin de deux chaussures, pas seulement d’une. » « Tu peux prendre un seul biscuit, mais pas deux. ») Certains enfants entrent en maternelle sans pouvoir reconnaître tous les nombres intuitifs. De tels enfants présentent un risque grave d’échec scolaire et ont besoin d’orthopédagogie intensive. À la maternelle, le dépistage doit vérifier si les enfants peuvent percevoir immédiatement des collections comptant entre un et trois objets et les distinguer de collections un peu plus nombreuses, comptant quatre ou cinq objets.

Comme l’illustre la figure 1, la co-évolution des concepts cardinaux des nombres intuitifs et l’aptitude à la reconnaissance visuelle des nombres peuvent jeter les bases de concepts et d’aptitudes variés concernant les nombres, le comptage et l’arithmétique, y compris la maîtrise des faits élémentaires d’addition et de soustraction. Les concepts relatifs aux petits nombres et la reconnaissance verbale des nombres peuvent fournir les bases pour le comptage verbal significatif. La perception des nombres intuitifs peut aider les enfants à voir littéralement qu’une collection désignée par « deux » compte davantage d’objets qu’une collection désignée par « un », et qu’une collection désignée par « trois » compte davantage d’objets qu’une collection désignée par « deux ». Cette compréhension ordinale de base des nombres, à son tour, peut aider les enfants à comprendre que l’ordre du nom des nombres importe lors du comptage (le principe d’ordre stable) et que la séquence des noms des nombres (« un, deux, trois... ») désigne des collections de plus en plus importantes. Au fur et à mesure qu’un enfant se familiarise avec la séquence de comptage, il développe la capacité de commencer à n’importe quel point dans la séquence et à indiquer (de façon efficace) le nom du nombre suivant dans la séquence (aptitude relative au nombre suivant) au lieu de compter à partir de « un ».

La capacité de nommer automatiquement le nombre qui vient tout de suite après un autre nombre dans la séquence de comptage peut constituer le fondement de la perception du fait qu’ajouter « un » à un nombre produit un nombre plus grand et, ce qui est plus important, de la règle du nombre suivant pour les faits n+1/1+n. Lorsqu’« un » est ajouté, la somme représente le nombre suivant l’autre nombre dans la séquence de comptage (c.-à-d. que la somme de 7+1 correspond au nombre suivant « sept » lors du comptage, soit « huit »).

Figure 1 : Trajectoire d’apprentissage de concepts et d’aptitudes clés en matière de nombres, de comptage et d’arithmétique

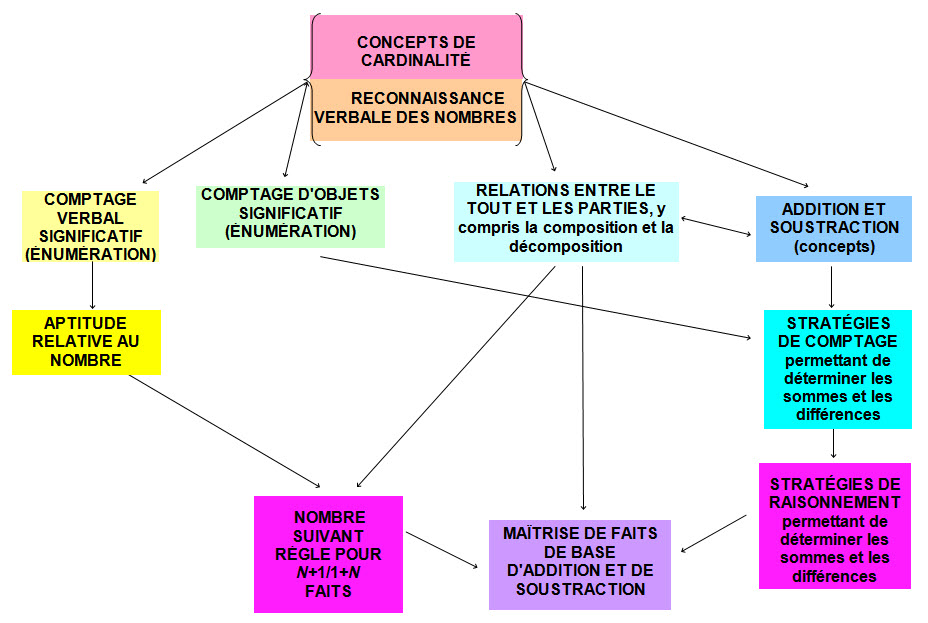
Cette stratégie de raisonnement peut permettre aux enfants de déduire de façon efficace la somme de toute combinaison semblable pour laquelle ils connaissent la séquence de comptage, même celles que les enfants n’ont pas encore répétées, telles que les faits d’addition de grands nombres à plusieurs chiffres comme 28+1, 128+1 ou 1 000 128+1. Avec le temps, cette stratégie de raisonnement devient automatique : elle peut être appliquée de façon efficace, sans délibération (c.-à-d. elle devient un élément du réseau de récupération en mémoire). Autrement dit, elle devient le fondement de la maîtrise des procédés pour les combinaisons n+1/1+n.

La reconnaissance verbale des nombres, et le concept de cardinalité qu’elle représente, peut constituer un fondement pour le comptage significatif d’objets.¹⁷ Les enfants qui peuvent subitiser des collections jusqu’à « quatre » sont plus susceptibles de bénéficier des efforts des adultes visant à démontrer et enseigner le comptage d’objets que ceux qui ne le peuvent pas. Lorsque le modelage consiste à compter et à étiqueter une collection dans la fourchette de subitisation des enfants, ils sont également plus susceptibles de reconnaître le but du comptage d’objets (une autre façon de déterminer le total d’une collection) et la justification des procédures de comptage d’objets (p. ex., la raison pour laquelle certaines personnes mettent l’accent sur le nom du dernier nombre utilisé lors du processus de comptage ou le répètent est qu’il représente le total de la collection).¹⁸ Le comptage significatif d’objets est nécessaire à l’invention de stratégies de comptage (avec des objets ou le nom des nombres), afin de déterminer les sommes et les différences. Au fur et à mesure que ces stratégies deviennent efficaces, l’attention est libérée et permet de découvrir des schémas et des relations; ces régularités mathématiques, à leur tour, peuvent devenir la base de stratégies de raisonnement (c.-à-d. le recours à des relations et à des procédés connus pour déduire la réponse à une combinaison inconnue). Au fur et à mesure que ces stratégies deviennent automatiques, elles peuvent devenir l’une des stratégies de récupération en mémoire qui permettront de produire des réponses de façon efficace à partir d’un réseau de mémoire ou de récupération en mémoire.

La reconnaissance verbale des nombres peut permettre à un enfant de voir qu’un plus un égalent deux, qu’un plus un plus un égalent trois, ou que deux plus un égalent trois, et le contraire (p. ex., trois égalent un plus un plus un ou deux plus un). L’enfant développe ainsi une compréhension de la composition et de la décomposition (un tout peut être bâti à partir d’éléments individuels ou décomposé en éléments individuels, souvent de différentes façons). Le fait de voir à de nombreuses reprises la composition et la décomposition de deux et de trois peut générer la maîtrise des procédés d’addition et de soustraction les plus simples (p. ex., « un plus un égalent deux », « deux plus un égalent trois », et « deux moins un égalent un »). La décomposition répétée de quatre et de cinq, avec de la rétroaction (p. ex., en désignant une collection de quatre comme étant « deux plus deux » et en entendant une autre personne confirmer que « oui, deux plus deux égalent quatre », peut générer une maîtrise des précédés jusqu’à cinq avec les sommes les plus simples, et représente une des façons de découvrir la règle du nombre suivant pour les combinaisons n+1/1+n (dont nous avons discuté précédemment).

Ensemble, le concept de cardinalité, la reconnaissance verbale des nombres et les concepts de composition et de décomposition peuvent fournir les fondements du développement d’un concept fondamental de l’addition et de la soustraction. Par exemple, en ajoutant un objet à une collection de deux objets, un enfant peut littéralement voir que la collection d’origine a été transformée en collection plus importante comptant trois objets. Ces compétences peuvent également fournir les fondements du développement d’une compréhension relativement concrète, et même relativement abstraite, des concepts arithmétiques suivants¹⁹ :

• Concept de la négation soustractive Par exemple, quand les enfants reconnaissent que lorsqu’on a deux blocs et qu’on enlève deux blocs, il ne reste aucun bloc, ils peuvent en déduire que tout nombre qui se soustrait lui-même ne laisse rien.
• Concept d’identité additive et soustractive Par exemple, quand les enfants reconnaissent que lorsqu’on a deux blocs et qu’on n’en enlève aucun, il reste deux blocs, ils peuvent déduire la régularité selon laquelle si on n’enlève rien d’un nombre, celui-ci ne change pas. Les concepts de négation soustractive et d’identité soustractive peuvent fournir les fondements de la maîtrise des procédés avec les familles de faits de soustraction respectives n-n=0 et n-0=n.

En conséquence, une faible perception des nombres peut nuire au développement de la maîtrise des procédés et à d’autres aspects des réalisations mathématiques. Par exemple, Mazzocco et Thompson²⁰ ont constaté que le rendement des enfants d’âge préscolaire sur les quatre éléments suivants du Test of Early Mathematics Ability – deuxième édition (TEMA-2) permettait de prédire quels enfants éprouveraient des difficultés en mathématiques en deuxième et en troisième années : le comptage significatif des objets (reconnaître que le dernier nombre utilisé lors du processus de comptage indique le total), la cardinalité, la comparaison de nombres d’un chiffre (p. ex., Lequel est le plus grand : quatre ou cinq?), l’addition mentale de nombres d’un chiffre et la lecture de nombres d’un chiffre. Notez que la reconnaissance verbale des nombres intuitifs est un fondement des trois premières aptitudes et un apprentissage significatif de la quatrième.

Question 4. La base consistant à aider les élèves à développer la perception des nombres en général et la maîtrise des faits en particulier crée des occasions leur permettant de découvrir des schémas et des relations. Par exemple, un enfant qui a appris les « doublons », tels que 5+5=10 et 6+6=12, d’une manière porteuse de sens (c.-à-d., l’enfant reconnaît que les sommes de cette famille sont toutes des nombres pairs), peut utiliser cette connaissance pour déduire les sommes de faits de doublons-plus-un inconnus, tels que 5+6 ou 7+6.

Pour être appropriées au développement de l’enfant, de telles occasions d’apprentissage doivent être ciblées, pertinentes et fondées sur le questionnement.²¹

• L’enseignement doit avoir un but et retenir l’attention des enfants. Cela peut être réalisé en intégrant l’enseignement à des jeux structurés (p. ex., un jeu consistant à lancer un dé peut aider les enfants à reconnaître les schémas réguliers entre un et six). Les leçons de musique et d’art peuvent servir de véhicules naturels pour la réflexion concernant les schémas, les nombres et les formes (p. ex., battre un rythme de deux ou trois, dessiner des groupes de ballons). Les parents et les enseignants peuvent tirer parti de nombreuses situations de tous les jours (p. ex., « Combien de pieds as-tu? ... Donc, combien de chaussettes faut-il sortir du tiroir? » Les questions des enfants peuvent représenter une source importante d’enseignement.
• L’enseignement doit être porteur de sens pour les enfants, et doit développer petit à petit ce qu’ils connaissent déjà (et y être lié). Un objectif significatif pour les adultes travaillant avec des enfants de deux ans est de faire reconnaître « deux » aux enfants. Le fait de les pousser trop rapidement à reconnaître des nombres plus importants, tel que quatre, peut être accablant et faire en sorte qu’ils se découragent (qu’ils deviennent inattentifs ou agressifs, qu’ils devinent n’importe quoi, ou qu’ils se désintéressent de l’activité).
• Dans la mesure du possible, l’enseignement doit être fondé sur l’interrogation ou susciter la réflexion. Au lieu de simplement donner des informations aux enfants, les parents et les enseignants doivent donner aux enfants l’occasion de réfléchir à un problème ou à une tâche, de conjecturer (faire des hypothèses bien fondées), de concevoir leurs propres stratégies ou de déduire leur propre réponse.

Les différents éléments ci-dessus sont illustrés par les cas d’Alice²² et de Lukas.²³

• Le cas d’Alice. Depuis plusieurs mois, la fillette de deux ans et demi pouvait reconnaître un, deux ou trois objets. Ses parents souhaitaient donc élargir ses connaissances jusqu’au nombre quatre, qui était tout près de ses compétences. Au lieu de simplement désigner des collections de quatre objets pour elle, ils l’ont interrogée concernant des collections de quatre objets. Alice réagissait souvent en décomposant les collections qu’elle ne reconnaissait pas en deux collections familières de deux objets chacun. Ses parents développaient alors sa réponse en lui disant, « Deux plus deux égalent quatre. » À 30 mois, lorsqu’on lui montra l’image de quatre chiots, Alice posa deux doigts de la main gauche sur deux chiots et dit : « Deux. » Tout en maintenant cette position, elle posa deux doigts de la main droite sur les deux autres chiots et dit : « Deux ». Elle eut ensuite recours à la relation connue « 2 plus 2 égalent 4 » (que ses parents lui avaient apprise) pour spécifier la cardinalité de la collection.
• Le cas de Lukas. Dans le cadre d’un jeu de mathématiques sur ordinateur, la question 6+6 fut présentée à Lukas. Celui-ci détermina la somme en comptant. Peu après, la question 7+7 lui fut posée. Il sourit et répondit, « Treize. » Lorsque l’ordinateur lui indiqua que la somme était en fait 14, il sembla perplexe. Quelques questions plus tard, la question 8+8 lui fut posée, et il remarqua : « J’allais dire 15, parce que 7+7 égalaient 14. Mais auparavant 6+6 égalaient 12, j’étais certain que 7+7 égalaient 13 mais c’était 14. Alors je vais dire que 8+8 égalent 16. »

Favoriser la maîtrise des opérations de soustraction : la méthode longue

Pour illustrer les implications des recherches récentes évoquées précédemment, examinons l’apprentissage de la maîtrise des opérations de soustraction de base les plus difficiles, telles que « 8 - 5 » et « 15 - 7 ». Les professeurs de mathématiques, les éditeurs de manuels scolaires et les décideurs en matière d’éducation recommandent couramment d’aider les enfants à apprendre ces opérations en leur faisant acquérir une stratégie de raisonnement qui appréhende la soustraction sous forme d’addition (par exemple, pour « 8 - 5 », il faut se dire : « Qu’est-ce qu’il faut ajouter à cinq pour faire huit? »).^24,25 La méthode courte, qui est trop souvent pratiquée, consiste à imposer (en illustrant ou en démontrant) la stratégie de raisonnement et dans certains cas à tenter de l’expliquer brièvement. Une pratique limitée de la stratégie est ensuite utilisée pour faire en sorte qu’elle devienne un automatisme. Le fait que nombre d’enfants ne comprennent pas la stratégie constitue une sérieuse limite de la méthode courte. En effet, cela peut les amener à la mémoriser sans pour autant parvenir à l’appliquer au moment opportun, voire à l’oublier complètement, ou encore à en mémoriser par cœur une version erronée ou à ne faire absolument aucun effort de mémorisation.

La méthode longue, qui consiste à utiliser l’addition comme stratégie de soustraction, ne saurait être enseignée en quelques jours, semaines, mois, ni même en un an. En effet, les expériences informelles et formelles des enfants les amènent souvent à penser que l’addition et la soustraction sont deux opérations qui n’ont aucun lien et que la connaissance de l’une ne peut pas contribuer à la compréhension de l’autre. La clé pour parvenir à maîtriser la différence de base entre ces deux opérations de manière significative et efficace, c’est (a) de découvrir le lien entre les opérations d’addition et de soustraction, (b) de maîtriser les sommes liées et (c) de s’entraîner à utiliser ces connaissances intégrées jusqu’à ce que le processus devienne automatiques.^26,27 Comme l’indique la trajectoire d’apprentissage décrite dans la figure 2, pour parvenir à une telle maîtrise, le processus de développement du sens des nombres se fait progressivement et dès l’âge préscolaire.

• Comme nous l’avons vu précédemment, la reconnaissance verbale des nombres fournit une base qui favorise une compréhension informelle du fait que l’addition constitue un moyen d’augmenter le nombre d’objets dans une collection et la soustraction un moyen de diminuer ce nombre (concept 1 de la figure 2). Ces concepts informels liés à l’addition et à la soustraction fournissent une base pour la compréhension et la résolution (informelle) de problèmes exprimés sous forme d’énoncés ou d’expressions symboliques telles que « 7 - 4 » et d’équations telles que « 7 - 4 = ? ».
• La reconnaissance verbale des nombres peut également servir de base à des expériences d’inversion empirique, c’est-à-dire des situations dans lesquelles quelques objets sont ajoutés (ou retirés) d’une petite collection, puis où le même nombre d’objets est ensuite retiré (ou ajouté) pour que la collection retrouve son nombre initial. Ces expériences peuvent aider les enfants à découvrir le concept d’annulation : l’addition et la soustraction sont liées parce qu’en ajoutant puis en soustrayant le même nombre d’éléments ou vice versa, on conserve le nombre initial d’éléments (concept 2 de la figure 4). Ce concept informel d’annulation fournit une base pour comprendre les représentations formelles (écrites) du concept, telles que « 7 + 4 - 4 = 7 » et reconnaître le concept relatif aux nombres partagés (à savoir le fait que des équations telles que « 7 + 4 = 11 » et « 11 - 4 = 7 » sont liées et partagent les trois mêmes nombres ; concept 4 de la figure 2).
• La reconnaissance verbale des nombres peut également aider les enfants à développer des concepts informels associés à la composition et à la décomposition (concept 3 de la figure 2), qui constituent la base d’une vision plus formelle de l’addition et de la soustraction en tant que rapport « partie-tout » (concept 4 de la figure 2). Cela permet aux enfants d’imaginer que deux collections (ou « parties ») qui sont petites et proches peuvent être considérées comme une seule collection plus grande (ou « tout ») ou bien qu’une seule collection plus grande peut constituer un tout formé de deux groupes plus petits (ou « parties »). Par exemple, le fait de voir un jet de dés affichant •• et •• comme un « deux » et un autre « deux » et de voir (ou d’entendre) un joueur plus âgé dire qu’il s’agit d’un « quatre » peut aider un enfant à comprendre que deux collections (plus petites) de « deux » peuvent être considérées comme des parties de la collection (plus grande) ou du tout « quatre », et que le tout « quatre » peut être décomposé en petites parties, à savoir « deux » et « deux ». En outre, le fait de considérer un jet de dés de • et de ••• comme un « un » et un « trois » et aussi comme un « quatre » au total peut aider les enfants à saisir que différentes combinaisons de collections ou de parties plus petites peuvent constituer le même nombre ou ensemble plus grand, ou bien qu’un ensemble peut être séparé en groupes ou parties plus petits. Une fois qu’ils ont appris à lire les nombres écrits, les enfants peuvent relier leurs connaissances informelles de la composition et de la décomposition à des expressions écrites telles que « 2 + 2 » ou « 1 + 3 »  et à des équations écrites telles que « 2 + 2 = 4 » ou « 1 + 3 = 4 » et développer les concepts formels suivants :
  • Plus précisément, les concepts informels de base de la composition et de la décomposition et les visions de type « partie-tout » peuvent servir de base à une interprétation formelle d’une équation d’addition telle que « 1 + 3 = 4 », car les parties 1 et 3 composent le grand tout 4 (par opposition à l’idée informelle selon laquelle une collection d’un seul élément est agrandie par l’ajout de trois autres) et « 4 - 3 = 1 », car le grand tout 4 est composé de la partie connue 3 et de la partie inconnue 1 (concept 5 de la figure 2 : connaissance formelle de l’addition et de la soustraction comme rapport « partie-tout »). Le fait d’envisager l’addition et la soustraction sous l’angle « partie-tout » permet de conclure que la soustraction d’une partie d’un tout laisse une partie plus petite que le tout.
  • Avant même que les enfants développent une vision de type « partie-tout » formelle de l’addition et de la soustraction (concept 5 de la figure 2), le fait de leur inculquer des notions informelles associées à la composition et à la décomposition peut les aider à mieux comprendre et formaliser le concept relatif aux nombres partagés, à savoir comprendre que les expressions écrites « 1 + 6 », « 2 + 5 », « 3 + 4 », « 4 + 3 », « 5 + 2 » et « 6 + 1 » ont toutes la même somme (tout), soit 7, et inversement, que le nombre (tout) 7 peut également être représenté par les expressions « 1 + 6 », « 2 + 5 », « 3 + 4 », « 4 + 3 », « 5 + 2 » et « 6 + 1 ». Pour ces deux raisons, « 1 + 6 », « 2 + 5 », « 3 + 4 », « 4 + 3 », « 5 + 2 » et « 6 + 1 » forment une « famille de sommes ». Il est important de noter que la compréhension de ce concept peut conduire à reconnaître que les familles de sommes sont liées aux familles de différences et que tous les membres de la famille sont constitués des trois mêmes nombres (concept relatif aux nombres partagés, illustré en tant que concept 4 de la figure 2).

Comme l’indique la trajectoire d’apprentissage décrite dans la figure 2, l’approfondissement de la compréhension de l’opération de soustraction et de sa relation avec l’addition, qui renforce les fondements de la maîtrise des différences de base, peut être réalisé à l’école maternelle et en première année.

• Le concept relatif aux nombres partagés peut être souligné en utilisant des « triangles d’informations », comme dans le programme Everyday Mathematics (voir par exemple, la figure 3 ou, pour plus de détails, voir Baroody²⁶). 
• La connaissance formelle de l’addition et de la soustraction en tant que rapport « partie-tout » peut être encouragée, en partie, en désignant explicitement les éléments d’un triangle de faits comme un « tout » ou une « partie » (par exemple, en utilisant un astérisque pour indiquer le « tout » ou en parlant de l’équation « 3 + 4 = 7 » en indiquant que « la partie trois et la partie quatre font un total de sept »). Les rectangles de faits peuvent fournir une représentation relativement concrète des relations « partie-tout » (voir par exemple la figure 4 ou, pour plus de détails, Baroody²⁶). La résolution d’énoncés de problèmes mettant en évidence le rapport « partie-tout » (voir par exemple la figure 5) peut également s’avérer utile.
• Mettre à la fois en avant le concept relatif aux nombres partagés et les connaissances formelles concernant le rapport « partie-tout » de manière intégrée peut favoriser la compréhension du concept selon lequel les parties et le tout sont partagés : Une famille d’opérations d’addition et de soustraction partage le même tout et les mêmes parties. Cette compréhension fournit une base pour reconnaître le principe de complément dont il est question dans le paragraphe suivant.

Comme le suggère la trajectoire d’apprentissage décrite dans la figure 2, les derniers éléments clés du développement de la stratégie de raisonnement par soustraction sous forme d’addition et de l’automatisation de cette stratégie peuvent maintenant être atteints en deuxième ou troisième année.

• La maîtrise des sommes de base jusqu’à 18 peut grandement faciliter l’utilisation de la stratégie de soustraction sous forme d’addition pour raisonner consciemment, puis de façon automatique dans le cadre des opérations de soustraction.
• La découverte du principe du complément, une autre relation clé entre l’addition et la soustraction (par exemple, si les parties 5 et 3 forment le tout 8, alors le tout 8 moins la partie 3 donne la partie 5), peut fournir une base pour comprendre pourquoi la stratégie de l’addition sous forme de soustraction fonctionne et permettre aux enfants de mieux l’assimiler.
• La stratégie consistant à appréhender la soustraction sous forme d’addition peut devenir automatique grâce à la pratique et permettre de maîtriser les différences jusqu’à 18.

Figure 2: Trajectoire d’apprentissage pour le développement constructif d’un raisonnement fondé sur la stratégie de soustraction dite de « soustraction sous forme d’addition »

Figure 3. Triangle de familles d’opérations

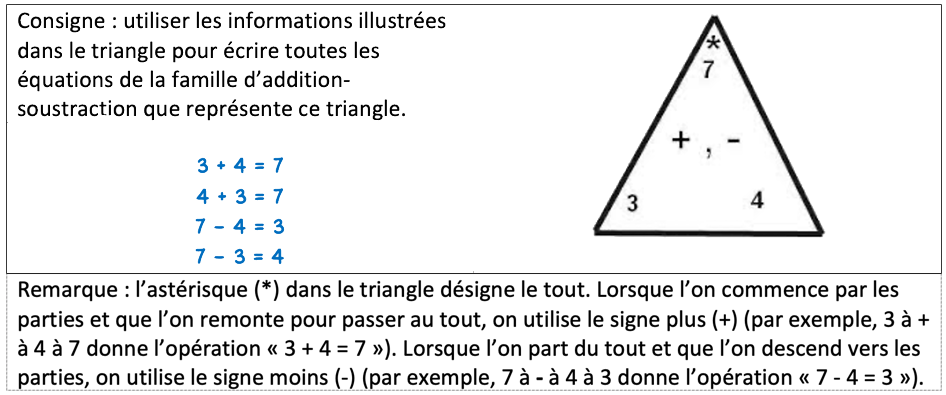
Figure 4. Rectangles d’informations

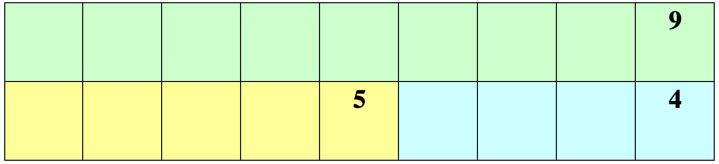
Figure 5 : Exemple d’énoncé de problème de type « partie-partie-tout »

Problème
Aza avait sept petits camions. Quatre étaient bleus et les autres étaient rouges. Combien de petits camions rouges avait Aza?

Illustration partie-partie-tout

Équation :   4 + ? = 7 or 7 – 4 = ?

Réponse :   3

Orientations futures

Il en reste encore beaucoup à apprendre concernant le développement des mathématiques chez les enfants d’âge préscolaire. L’aptitude à la reconnaissance verbale des nombres à deux ans permet-elle de prédire s'il sera prêt pour la maternelle la maternelle ou s'il réussira bien académiquement en mathématiques? Dans l’affirmative, une intervention ciblée sur les exemples et sur les contre exemples permet-elle aux enfants à risque d’échec scolaire de rattraper leurs camarades? Quels autres concepts ou quelles autres aptitudes, à l’âge de deux ou de trois ans, permettent de prédire s'il sera prêt pour la maternelle ou s'il réussira bien académiquement en mathématiques? Quelle est l’efficacité des programmes de mathématiques pour la petite enfance qui sont actuellement en cours de développement?

Conclusions

Contrairement aux convictions de certains éducateurs de la petite enfance, l’enseignement des mathématiques pour les enfants ayant aussi peu que deux ans est sensé.^22,28,30,31 Tel que l’illustre clairement la figure 1, l’enseignement doit commencer par aider les enfants à développer un concept cardinal des nombres intuitifs, ainsi que l’aptitude à reconnaître et à désigner des ensembles d’un à trois objets au moyen du nom du nombre approprié. Comme l’illustre également la figure 1, ces aspects de la connaissance des nombres sont des éléments clés pour la numératie par la suite et sont souvent absents chez les enfants présentant des déficiences en mathématiques.³² Par exemple, bien que la mémorisation de l’opération de base qu’est la soustraction soit souvent problématique, voire difficile ou inaccessible pour de nombreux enfants, il peut en être autrement si l’enseignement aide les enfants à développer le sens des nombres en découvrant des régularités arithmétiques clés aux niveaux préscolaire et primaire. L’enseignement précoce ne signifie pas d’imposer des connaissances aux enfants d’âge préscolaire, de les faire répéter avec des cartes-éclair, ou de leur faire apprendre par cœur des procédés arithmétiques. L’encouragement de la perception des nombres et de la maîtrise des faits est axé sur le fait d’aider les enfants à découvrir les schémas et les relations et de les encourager à inventer leurs propres stratégies de raisonnement.

L’étude décrite a été partiellement financée par une subvention de la National Science Foundation (BCS-0111829), de la Spencer Foundation (Major Grant 200400033), des National Institutes of Health (1 R01 HD051538-01) et de l’Institute of Education Science (R305K050082 et R305A080479).  La révision de ce rapport a été soutenue par des subventions de la National Science Foundation (1621470 et 2201939). Les opinions exprimées dans le présent manuscrit sont exclusivement celles de l’auteur et ne reflètent pas nécessairement la position ou les politiques des institutions susmentionnées ou ne bénéficient pas nécessairement de leur aval.

Références

1. Baroody AJ, Lai ML, Mix KS. The development of number and operation sense in early childhood. In: Saracho O, Spodek B, eds. Handbook of research on the education of young children. Mahwah, NJ: Erlbaum; 2006: 187-221.
2. Clements D, Sarama J, DiBiase AM, eds. Engaging young children in mathematics: Standards for early childhood mathematics education. Mahwah, NJ: Lawrence Erlbaum Associates; 2004: 149-172.
3. Ginsburg HP, Klein A, Starkey P. The development of children’s mathematical knowledge: Connecting research with practice. In: Sigel IE, Renninger KA, eds. Child psychology in practice. 5th Ed. New York, NY: Wiley & Sons; 1998; 401-476. Handbook of child psychology, vol 4.
4. Baroody AJ, Dowker A. The development of arithmetic concepts and skills: Constructing adaptive expertise. In: Schoenfeld A, ed. Studies in mathematics thinking and learning series. Mahwah, NJ: Lawrence Erlbaum Associates; 2003.
5. Kilpatrick J, Swafford J, Findell B, eds. Adding it up: Helping children learn mathematics. Washington, DC: National Academy Press; 2001.
6. Baroody AJ, Bajwa NP, Eiland M. Why can’t Johnny remember the basic facts? Developmental Disabilities Research Reviews 2009;15(1):69-79. (Special issue on “Pathways to Mathematical Learning Disabilities,” guest edited by M. Mazzocco.) doi:10.1002/ddrr.45
7. Baroody AJ, Purpura DJ. Early number and operations: Whole numbers. In: Cai J, ed. Compendium for research in mathematics education. Reston, VA: National Council of Teachers of Mathematics; 2017:308-354.
8. Gersten R, Chard, D. Number sense: Rethinking arithmetic instruction for students with mathematical disabilities. The Journal of Special Education 1999;33(1):18–28.
9. Jordan NC. The need for number sense. Educational Leadership. 2007;65(2):63-66.
10. Dowker AD. Individual differences in arithmetic: Implications for psychology, neuroscience and education. Hove, England: Psychology Press; 2005.
11. Baroody AJ. The development of kindergartners' mental-addition strategies. Learning and Individual Differences 1992;4:215-235.
12. Baroody AJ, Eiland M, Thompson B. Fostering at-risk preschoolers' number sense. Early Education and Development 2009;20:80-120.
13. Mix KS, Sandhofer CM, Baroody AJ. Number words and number concepts: The interplay of verbal and nonverbal processes in early quantitative development. In: Kail R, ed. Advances in child development and behavior, vol 33. New York, NY: Academic Press; 2005: 305-346.
14. Baroody AJ, Li X, Lai ML. Toddlers’ spontaneous attention to number. Mathematics Thinking and Learning 2008;10:1-31.
15. Dehaene S. The number sense. New York, NY: Oxford University Press; 1997.
16. Wynn K. Numerical competence in infants. In: Donlan C, ed. Development of mathematical skills. Hove, England: Psychology Press; 1998:1-25.
17. Benoit L, Lehalle H, Jouen F. Do young children acquire number words through subitizing or counting? Cognitive Development 2004;19:291-307.
18. Paliwal V, Baroody AJ. Cardinality principle understanding: The role of focusing on the subitizing ability. ZDM Mathematics Education 2020;52(4):649-661. doi:10.1007/s11858-020-01150-0
19. Baroody AJ, Lai ML, Li X, Baroody AE. Preschoolers’ understanding of subtraction-related principles. Mathematics Thinking and Learning 2009;11:41-60.
20. Mazzocco M, Thompson R. Kindergarten predictors of math learning disability. Learning Disabilities Research & Practice 2005;20:142-155.
21. Baroody AJ, Coslick RT. Fostering children's mathematical power: An investigative approach to K-8 mathematics instruction. Mahwah, NJ: Erlbaum; 1998.
22. Baroody AJ, Rosu L. Adaptive expertise with basic addition and subtraction combinations: The number sense view. In: Baroody AJ, Torbeyns T. chairs. Developing Adaptive 
    Expertise in Elementary School Arithmetic. Symposium conducted at: The annual meeting of the American Educational Research Association. April, 2006. San Francisco, CA.
23. Baroody AJ. Fostering early number sense. Keynote address at: The Banff International Conference on Behavioural Science. March, 2008. Banff, Alberta.
24. National Council of Teachers of Mathematics. Curriculum focal points for prekindergarten through grade 8 mathematics. Reston, VA: Author; 2006.
25. National Governors Association Center for Best Practices and Council of Chief State School Officers. Common Core State Standards: Preparing America’s students for college and career.
26. Baroody AJ. Curricular approaches to introducing subtraction and fostering fluency with basic differences in grade 1. In: Bracho R, ed. The development of number sense: From theory to practice. Monograph of the Journal of Pensamiento Numérico y Algebraico [Numerical and Algebraic Thought] 2016;10(3):161–191. University of Granada.
27. Baroody A J, Purpura D J, Eiland MD, Reid EE, Paliwal V. Does fostering reasoning strategies for relatively difficult basic combinations promote transfer? Journal of Educational Psychology 2016;108: 576–591. doi: 10.1037/edu0000067
28. Baroody AJ, Li X. Mathematics instruction that makes sense for 2- to 5-year-olds. In: Essa EA, Burnham MM, eds. Development and education: Research reviews from young children. New York: The National Association for the Education of Young Children; 2009: 119-135.
29. Bredekamp S, Copple C. Developmentally appropriate practice in early childhood programs. Washington, DC:  National Association for the Education of Young Children; 1997.
30. Copley J, ed.  Mathematics in the early years, birth to five. Reston, VA: National Council of Teachers of Mathematics; 1999.
31. Copley J, ed. The young child and mathematics. Washington, DC: National Association for the Education of Young Children; 2000.
32. Landerl K, Bevan A, Butterworth B. Developmental dyscalculia and basic numerical capacities: A study of 8–9-year-old students. Cognition 2004;93:99-125.